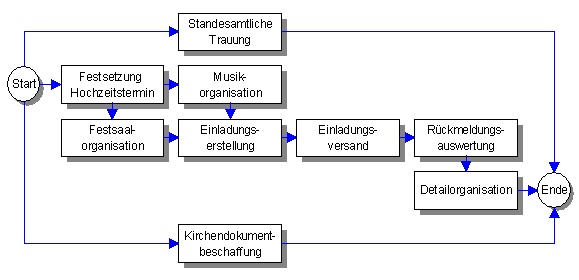
Beispiel eines Netzplanes
2 Fahrplandarstellung mit Hilfe der Netzplantechnik |
Ein Fahrplan beschreibt Teilverbindungen sowie (explizit und implizit) deren Verknüpfungsmöglichkeiten untereinander. Teilverbindungen sind nun aber nichts anderes als zeitlich festgelegte Vorgänge. Eine etablierte, aus dem Projektmanagement kommende Technik zur Abbildung solcher Vorgänge und deren gegenseitiger Abhängigkeiten ist die Netzplantechnik.
Zu Beginn ist hier noch eine Definition des Begriffes Projekt wiedergegeben:
| Ein Projekt ist ein Vorhaben, das eine klar definierte Aufgabenstellung sowie definierte Anfangs- und Endzeitpunkte hat. |

Beispiel eines Netzplanes
Ein Netzplan ist ein Graph. In der hier verwendeten Darstellung als Vorgangsknotennetz werden die Vorgänge durch Knoten, die sogenannten Vorgangsknoten, und die Abhängigkeiten zwischen den Vorgängen durch Kanten dargestellt. So sind die zeitlichen Abhängigkeiten der einzelnen Vorgänge genau ersichtlich. Es können beispielsweise vor der Saalbeschaffung keine Einladungen erstellt werden. Diese Abhängigkeiten werden auch als Anordnungsbeziehungen bezeichnet. Eine Anordnungsbeziehung verbindet einen Vorgängerknoten mit einem Nachfolgeknoten.
![]()
Normalfolge
Die drei anderen Arten von Anordnungsbeziehungen sind die Anfang-Anfang-Beziehung oder Anfangsfolge, die Ende-Ende-Beziehung oder Endfolge sowie die Anfang-Ende-Beziehung oder Sprungfolge. Sie sind der Vollständigkeit halber hier erwähnt, es wird aber in dieser Arbeit nicht weiter darauf eingegangen. Ebensowenig wird hier auf die Möglichkeit eingegangen, statt Mindestabständen Maximalabstände anzugeben.
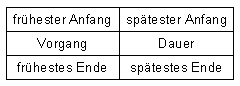
Die Bedeutung der einzelnen Felder für die Anfangs- und Endzeiten
soll nun erläutert werden. Die Zeiten werden in weiterer Folge beispielhaft
in Tagen angegeben.
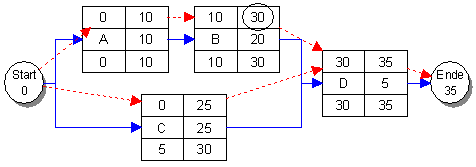
Frühestmögliche Anfangs- und Endzeiten
Das Projekt startet am Tag 0, dies ist der frühestmögliche Beginn der beiden Vorgänge A und C. Frühestens am 10. Tag ist Vorgang A abgeschlossen, dies ist der frühestmögliche Beginn für Vorgang B, der am frühestens 30. Tag abgeschlossen ist. Vorgang C ist frühestens am 25. Tag beendet. Vorgang D kann aber erst gestartet werden, wenn auch Vorgang B abgeschlossen ist, das ist frühestens am 30. Tag der Fall.
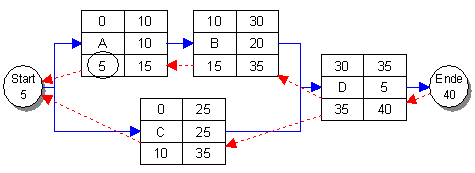
Spätestzulässige Anfangs- und Endzeiten
Das Projekt soll spätestens am 40. Tag beendet werden, dies ist das spätestzulässige Ende des Vorganges D. Dieser Vorgang muß daher spätestens am 35. Tag beginnen, das ist gleichzeitig das späteste Ende der beiden Vorgänge B und C. Spätestens am 15. Tag ist Vorgang B zu beginnen, dies ist das späteste Ende für Vorgang A, der daher spätestens am 5. Tag starten muß. Vorgang C muß spätestens am 10. Tag in Angriff genommen werden. Das Projekt muß spätestens am 5. Tag beginnen, entscheidend hierfür ist die spätestzulässige Anfangszeit von Vorgang A.
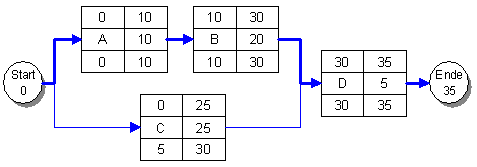
Kritischer Weg
Das Projekt startet also am Tag 0 und endet am Tag 35. Der Vorgang A dauert 10 Tage, der Vorgang B dauert 20 und der Vorgang D benötigt 5 Tage. Diese drei Vorgänge bestimmen also die Gesamtdauer des Projektes und ergeben den kritischen Weg. Der Vorgang C benötigt 25 Tage. Da mit seinem Nachfolger wegen der Vorgänge A und B aber erst am 30 Tag begonnen werden kann, ergibt sich für Vorgang C ein Spielraum von 5 Tagen. Erst ab einer Verschiebung oder Verlängerung des Vorganges C von mehr als 5 Tagen wirkt sich das auf das Projektende aus. Diesen Spielraum nennt man Pufferzeit.
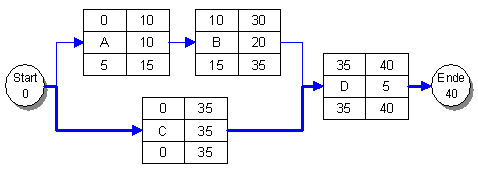
Gesamte Pufferzeit
Der kritische Weg verläuft nun durch den Vorgang C, die Vorgänge A und B erhalten nun Pufferzeiten von 5 Minuten. Diese Pufferzeit steht aber innerhalb des unkritischen Weges nur einmal zur Verfügung, wird sie also beispielsweise in Vorgang A bereits aufgebraucht, so steht Vorgang B nichts mehr von dieser Reserve zur Verfügung. In der Netzplantechnik sind daher noch weitere Arten von Pufferzeiten in Gebrauch, auf die hier aber nicht weiter eingegangen werden soll.
In dieser Arbeit steht nicht die Erstellung eines neuen Fahrplanes im Mittelpunkt. Es soll vielmehr ein bestehender Fahrplan zum Zwecke der Verbindungssuche ausgewertet werden. Es stellt sich somit nicht mehr die Frage nach den frühestmöglichen und spätestzulässigen Abfahrts- und Ankunftszeiten einzelner Teilverbindungen, stattdessen stehen die konreten Zeiten bereits fest. Ein kleiner Fahrplanausschnitt zeigt das Prinzip:
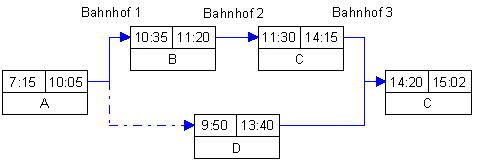
Fahrplandarstellung als Netzplan
Zug A erreicht Bahnhof 1 um 10:05. Dort kann in Zug B umgestiegen werden.
In weiterer Folge wird in Bahnhof 2 in Zug C umgestiegen, der dann mit
Halt in Bahnhof 3 durchfährt. Zug D kann von Zug A aus nicht mehr
erreicht werden. Die strichliert gezeichnete Normalfolge ist hier also
nicht erfüllbar. Zug A hält außerdem nicht in Bahnhof 2,
eventuell befährt er zwischen Bahnhof 1 und Bahnhof 3 sogar eine andere
Strecke.
Bei Anordnungsbeziehungen muß zwischen einem reinen Zwischenhalt
und einem echten Umsteigevorgang unterschieden werden. Bei einem Umsteigevorgang
muß beurteilt werden können, ob ausreichend Zeit zum Umsteigen
zur Verfügung steht. Zu diesem Zweck werden die Anordnungsbeziehungen
mit Mindestabstandszeiten versehen. Die Mindestabstandszeiten hängen
von unterschiedlichen Faktoren wie beispielsweise den Bahnsteigentfernungen
oder einer Zollabfertigung auf dem Umsteigebahnhof ab. Darauf wird später
noch eingegangen.
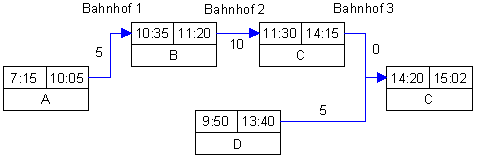
Mindestzeiten für Umsteigevorgänge
Von Zug A nach Zug B gibt es keine Probleme, einer Mindestabstandszeit von zehn Minuten steht ein tatsächlicher Abstand von einer halben Stunde gegenüber. Beim Umsteigen von Zug B nach Zug C kann es hingegen eng werden, dieser Umsteigevorgang ist als kritisch anzusehen. In weiterer Folge ist in Bahnhof 3 der Mindestabstand gleich Null, da hier kein Umsteigevorgang stattfindet und somit auch keine Zeitreserve eingeplant werden muß. Reisende, die von Zug D kommend in Zug C umsteigen, müssen aber wiederum fünf Minuten Mindestabstand einhalten, was hier auch erfüllt wird.
Natürlich sind auch Anschlüsse denkbar, die in einer direkten oder indirekten Rüchfahrt zu einem bereits passierten Bahnhof resultieren. Dennoch ergeben sich dadurch noch keine Zyklen.
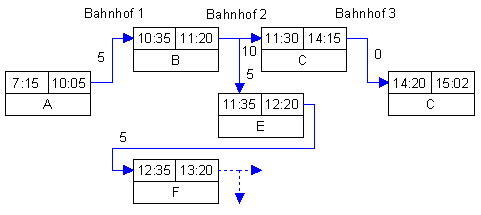
Anschluß als Rückfahrt
Der Zug B begegnet in Bahnhof 2 seinem Gegenzug E, der natürlich
auch einen gültigen und nutzbaren Anschluß darstellt. Zurück
in Bahnhof 1 kann natürlich nicht mehr in Zug B umgestiegen werden,
wohl aber in einen seiner Nachfolger, hier Zug F. Dieses Spielchen könnte
man nun beliebig lange fortsetzen, der Netzplan würde dabei immer
umfangreicher.
In der Regel wird sich der Fahrplan (von Ausnahmen abgesehen) irgendwann wiederholen, beispielsweise nach 24 Stunden. Im Falle von Taktfahrplänen kann dies aber auch schon nach einer Stunde oder sogar nach wenigen Minuten der Fall sein. Zur Vereinfachung kann man daher die Zyklenfreiheit aufgeben und eine sich periodisch wiederholende Teilverbindung nur einmal darstellen.
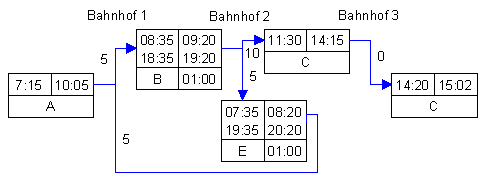
Wiederholende Teilverbindungen als Zyklus
Die Züge B und E verkehren jeweils im Einstundentakt, diese Taktzeit ist nun zusätzlich angegeben. Weiters werden statt der konkreten Abfahrts- und Ankunftszeiten einer bestimmten Teilverbindung nur noch jeweils die der ersten und letzten Verbindung angegeben. Man kann hier erkennen, daß alle Wiederholungen des Zuges B mit den Abfahrtszeiten 8:35 bis 10:35 und somit den Ankunftszeiten 9:20 bis 11:20 geeignet sind, als Zubringer für Zug C zu fungieren.
Sowohl bei individuellen als auch bei vertakteten Teilverbindungen können weitere Angaben zur Gültigkeit (z.B. Verkehrstage) gemacht werden. Variierende oder abwechselnde Takte werden einfach durch parallele Teilverbindungen dargestellt.
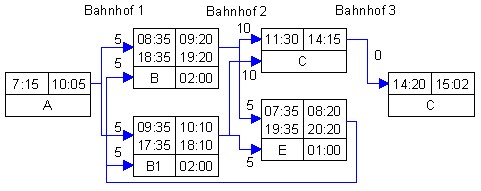
Variierende Taktverbindungen
Hier wechseln sich stündlich der Zug B und der etwas schnellere
Zug B1 ab. Es wurde angenommen, daß die Abfahrts- und Endbahnsteige
und alle sonstigen örtlichen Gegebenheiten dabei unverändert
bleiben. Dies drückt sich in den gleichen Mindestabstandszeiten für
beide Teilverbindungen aus.